Week 6 PSET
PSET #6
ASSIGNED: Friday 15 May 2020
DUE: Tuesday 26 May 2020 5:00 PM Pacific
NOTES:
- Given the unique circumstance of Spring 2020, we ask you to do your best to maximize your learning. Each problem set is an opportunity to assess your learning, identify gaps, reflect on what you have learned, and determine what you wish to learn next.
- You can discuss the PSET questions with other students. But your answers should be your own work. Please let us know if you collaborated with other students working on the PSET.
- Please turn in your completed problem sets as an electronic copy via Gradescope. Please make sure to clearly indicate the starting and ending boundaries of your answers to each question on Gradescope.
- Please do not go over any word limits.
- Please type your answers.
- Please label and provide descriptions for the figures.
- Please show your work and include units.
(Q1) Diffusion, Diffusion constant, and Diffusion time (30 pts)
In this question you will explore diffusion both qualitatively and quantitatively.
First let’s warm up:
The diffusion coefficient is described by the following equation: $D=\frac{k_BT}{6\pi \eta a}$
- $k_B$ is Boltzmann’s constant 1.3807 x 10 ^-23 $ \frac{J}{K} $
- $T$ is the temperature (K) of the surrounding medium ,
- $\eta$ is viscosity of surrounding medium $ \frac{N \cdot s}{m^2} $,
- $a$ is a measure of length (radius of a sphere approximating the molecule).
1.a. Using the facts above determine the units for diffusion coefficient (show your work):
You learn that the diffusion coefficient for a protein (green fluorescent protein, GFP) in water is about 100 µm^2/s. But, the diffusion coefficient for the same protein in the cytoplasm of a living cell is only 30 µm^2/s.
1.b. Intuitively do these numbers make sense? (Yes or No) Why? (Bullet points)
Next, let’s estimate the time it takes for a protein to diffuse spontaneously across different types of cells (diffusion time τ).
- We will use the formula $\tau =\frac{R^2}{6D} $, where $R$ is the traverse distance.
1.c. Calculate the times it takes for the GFP protein with a diffusion constant D=30 µm^2/s to diffuse across four different cell types:
-
(i) E.coli with R≈1 μm,
-
(ii) Yeast cell with R≈10 μm,
-
(iii) HeLa cell with R≈20 μm,
-
(iv) A neuronal cell axon with R≈1 cm.
1.d. Create a $\tau$ vs $R$ plot (use the above four cases).
1.e. What does the the diffusion time for the axon suggests to you in terms of how axons work?
This question is from the Cell Biology by the Numbers
(Q2) Diffusion and Spatial DNA devices (20 pts)
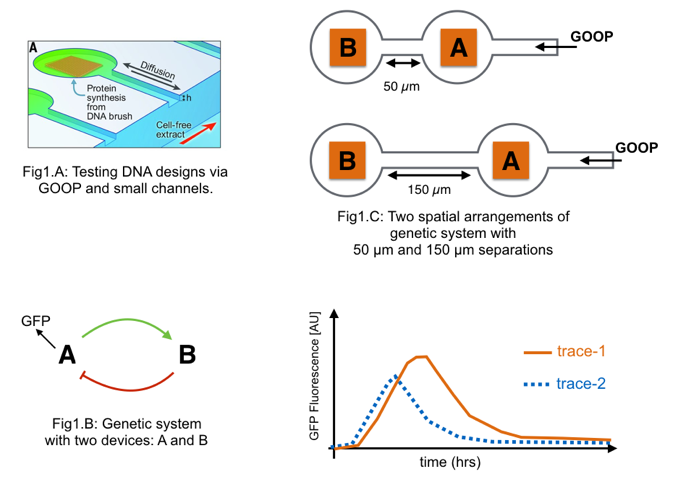
Two DNA devices have been engineered for use in a cell-free extract (i.e., a “goopy” solution derived from living cells, aka “GOOP”) (Figure, below). Bioengineered DNA-based devices placed into the extract will have their encoded DNA transcribed into mRNA and the mRNA translated into protein.
-
Device A expresses protein A in the absence of protein B.
-
Device B expresses protein B in the presence of protein A.
-
Device A can also make GFP.
Each device is placed in a distinct reservoir within a micro-scale fluidic channel.
Fresh extract is supplied from one end of the channel. Using various channel lengths experimenters are testing a genetic system made from the two devices.
2.a. By studying the diagram in Figure 1.B, describe the expected relationships and behavior of the system.
(1-2 sentences max)
2.b. Figure 1.C shows two spatial arrangements of the genetic system. In the top arrangement device A is 50 µm away from device B. In the lower arrangement device A is 150 µm away from device B. The time responses for each arrangement is measured by GFP production from device A as presented below. Does “trace-1” come from the 50 µm or 150 µm arrangement?
2.c. Explain your choice. (Hint: think about diffusion) (1-2 sentences max or math)
(Q3) Bacterial Edge Detection (20)
We have talked about engineered E.coli which detects light earlier in the quarter.
Building on earlier work first published in 2005, Jeff Tabor and colleagues eventually demonstrated a bacterial edge detection system.
In their system a bacterial lawn (i.e., a uniform layer of identically engineered bacteria growing on a plate) detect a light-encoded image. The bacteria are initially all the same but, depending on whether they are exposed to light or not, send or receive small molecule-encoded signals that diffuse across the light/dark boundary.
Only bacteria positioned at the boundary between light and dark express an enzyme that results in formation of a dark pigment (HINT: see Figure and also the primary source article).
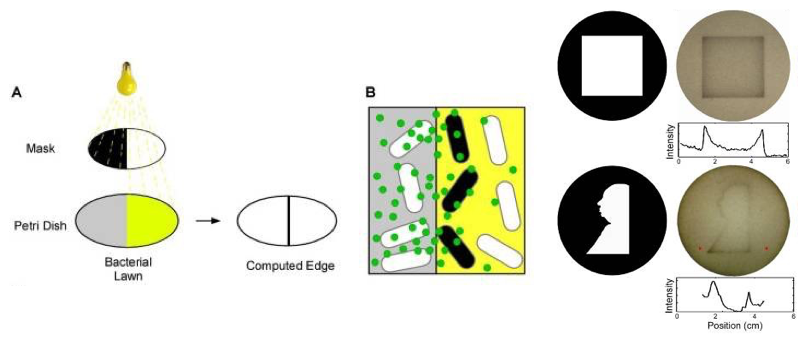
Carefully study the photo of the system in action. Note various details about the edge detection beahvoir in the case of a square or Alfred Hitchcock’s portrait.
3.a. What do you observe? Are all the edges uniform? (1-2 sentences)
3.b. Using concepts from this week, why is there more pigment inside the corners of the square, or inside the bottom left angle of Alfred’s portrait?
(Q4) Regrowing a newt arm (30 pts)
Please watch this video of a newt regrowing its arm.
How does this work? Let’s apply the concepts we’ve learned from dancing droplets challenges to figure this out from a programming patterns perspective.
Q.4.a. “The hand of god”
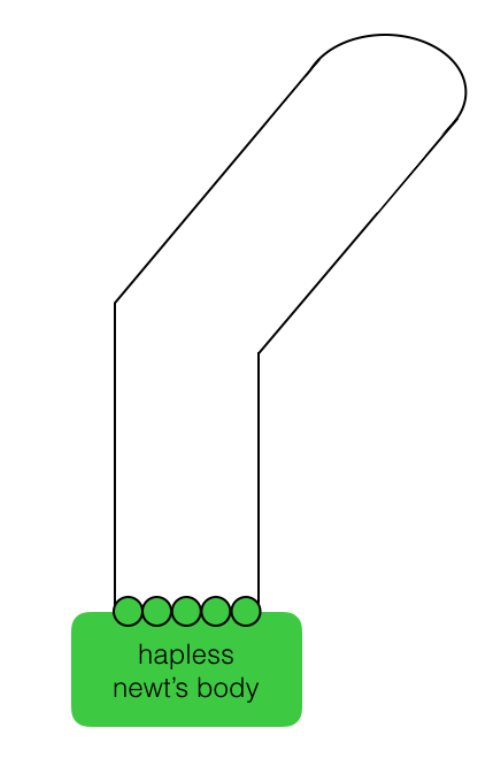
Pictured below is a newt’s body with five regenerative cells (green circles) that are ready to regenerate a limb. You are a sculptor of limbs and create a physical scaffold that outlines and limits the aggregate shape that the cells should grow into. The cells just need to grow into the shape that you’ve defined (the simple “bent-arm” solid line trace).
What do the cells need to do in order fill the physical form you have preshaped for them?
Q.4.b. “Celestial navigation”
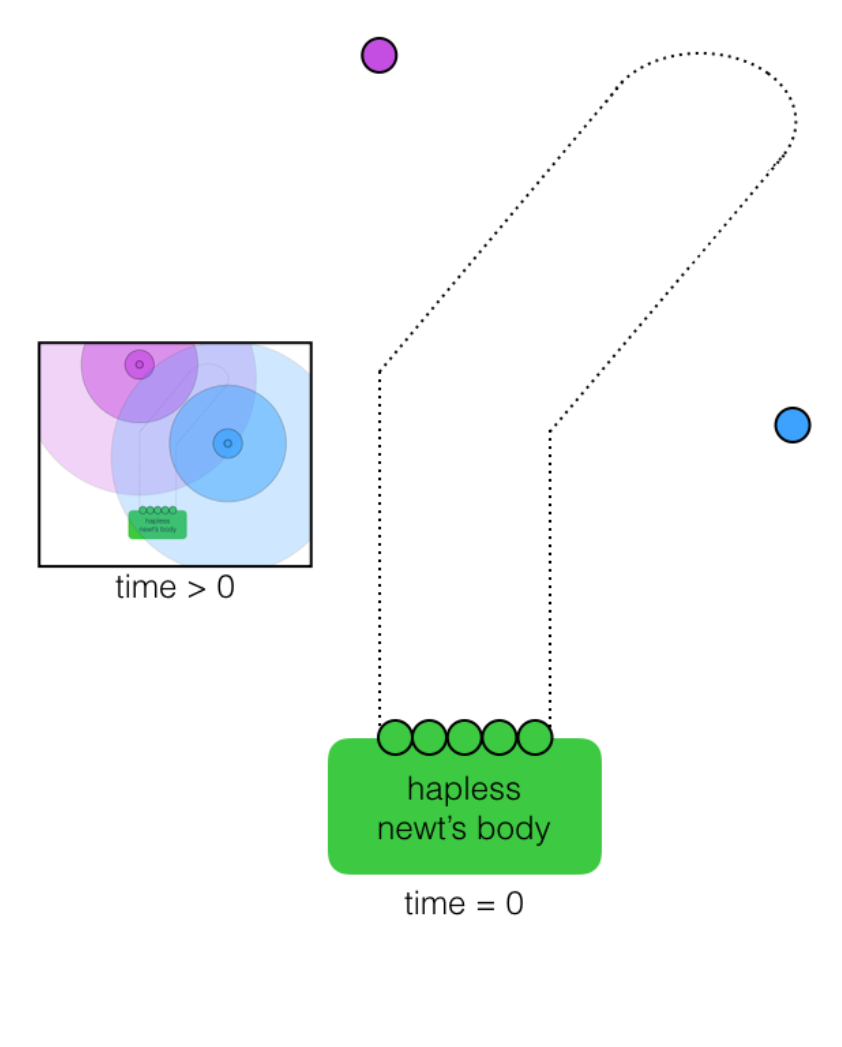
Next, consider a different set of starting conditions: You no longer exist.
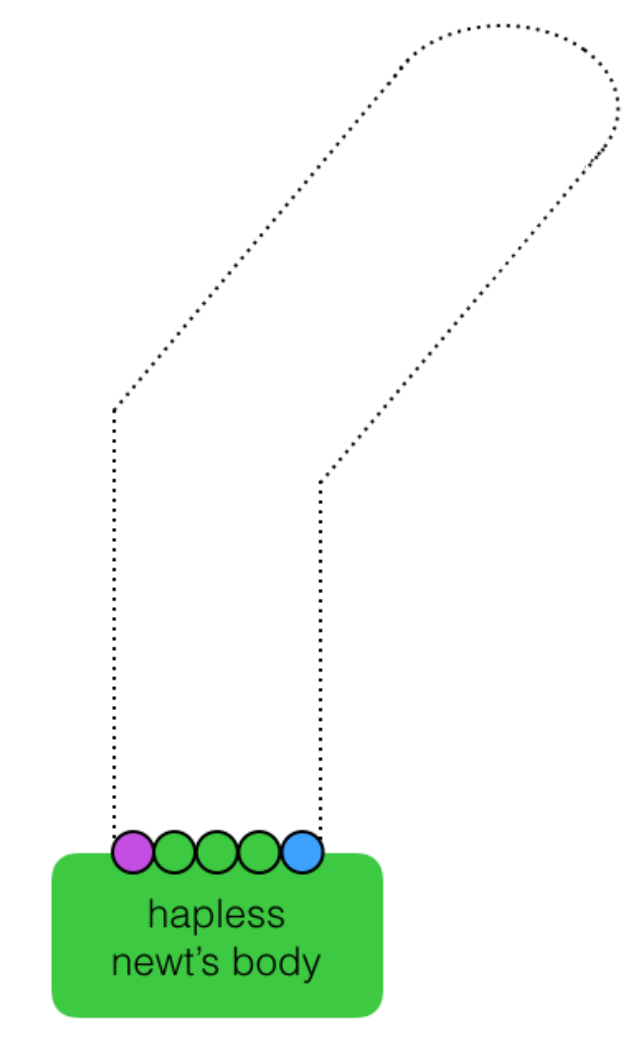
In the picture below, the newt still has to regrow its arm into the shape indicated by the faint dotted line, but this time, without your barrier into which the cells could simply grow. However, two external beacon cells (purple and blue) have been added to the system. Each beacon cell emits a distinct and freely diffusing small molecule (see “time > 0 inset) that the regenerative cells (green) can detect and respond to using the following programmed functions:
move, divide, sense, attract, repel, change color, count cell divisions
Describe how the five green cells can use their programmed functions to grow into the desired pattern in response to the signals initially emanating from the external beacons.
Q.4.c. “Full autonomy”
Finally, pictured below is a newt that needs to regrow its arm using only its own regenerative cells (there are no external inputs to the system). The two outside regenerative cells have differentiated into distinct left and right cells (below).
Describe how the five originating cells (purple, green, green, green, blue) can use their programmed functions to grow into the desired pattern by themselves, using no outside information or control.
Q.4.d. Applications
The concept of using gradients to drive the behavior of autonomous devices can be observed in many other applications besides newt arm regeneration.
Briefly describe (in 1-2 sentences) another application of this concept: where else is this behavior seen and how does it relate?
Final Project - Group Activity.2 (10 points)
NOTES:
-
Due: Next Tuesday (with PSET)
-
Include your group number, names of your group members, and name of your digital (TA) mentor.
-
Please turn in a single electronic copy of your Group Activity via Gradescope.
Group Activity.2.a. Please share your team’s top selection for the final project.
Group Activity.2.b. Please share two back-up selections for the final project.
Group Activity.2.c. Why did your team select your top choice? (about 150 words)
Group Activity.2.d. How did you reach your decision? Please also include each individual team member’s “bang for your buck” (effort v. impact) plot. (about 150 words)
Additional Questions and Resources
(Q5) Paper reading activity (0 pts)
First examine, A synchronized quorum of genetic clocks.
Q.5.a In your own words, what is the primary claim of the paper? What are the primary evidence in support of the claim? (2-3 sentences)
Q.5.b In your opinion, what are the paper’s strengths and significance? What are the paper’s shortcomings and deficiencies? How can the paper improve?
(Q6) Dancing Droplets (0 pts)
On Wednesday you experienced (or read about) the the Dancing Droplets. Use pictures, diagrams, or drawings as appropriate.
6.a. What rule did you observe (or read) about - which droplets chase which?
6.b. Why does the sharpie marker create a physical barrier and how do the droplets respond to it?
6.c. To what extent were you able to realize increasingly autonomous behavior?
6.d. How would you use autonomous behaviors (with droplets or cells) to generate pattersn? What patterns will you build - what will they do? How good do we have to become at implementing autonomous behaviors to achieve your patterns? (2-3 sentences)
Extra-activity Make your own dancing droplet video (30 to 60 seconds) with your own choice of background music and share a link with us.
The following link takes you to a paper titled Life at Low Reynolds Number that examines physics at the scale of a bacteria.
The following links are explorables that can help you explore and build an intuition about patterns and pattern formation. We hope that you take some time and examine them on your own:
github source code for teaching staff